מבחני צורות הם מבחנים שלא נתקלים בהם בתוכנית הלימודים הרגילה, אלא רק במבחני קבלה פסיכוטכניים לבתי ספר ולתוכניות לאיתור מחוננים (לתלמידי כיתות ז'-י'). מבחנים אלו בודקים יכולות אנליטיות ואינטגרטיביות שונות, ויש להם משקל גדול בציון הסופי.
בעמוד זה נציג את שני הנושאים העיקריים במבחני הצורות הפסיכוטכניים - מטריצות וצורות בשורה וגם תקבלו הצצה למבחן צורות לדוגמא חינם (pdf). כך תוכלו להתנסות בשאלות לדוגמא, ללמוד שיטות פתרון רלוונטיות, ולהגיע מוכנים יותר למבחנים.
מטריצות
סוג זה של שאלות כולל לרוב שמונה צורות, המסודרות בשלוש שורות ובשלושה טורים, וההוראה היא להשלים את הצורה החסרה. כדי לענות על השאלה, יש לזהות את החוקיות הקיימת במטריצה, ולנסות להבין אילו מרכיבים קיימים בצורה החסרה.
נתמקד בשני סוגים של מטריצות: "איחוד/חיתוך" ו"תזוזה/תנועה"
ובשתי שיטות לפתרון: "הפרדת אלמנטים" ו"בדיקת חוקיות" (בהמשך).
מטריצות: איחוד/חיתוך
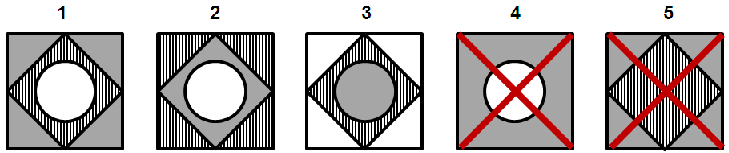
שאלות רבות במבחן המטריצות הן מסוג איחוד/חיתוך. בשאלות אלו, יש להשתמש בטכניקה בסיסית, שבה אנו מחברים/מאחדים שתי צורות כדי לקבל צורה שלישית. הצורה המחוברת יכולה להיות הצורה הראשונה, השנייה או השלישית בשורה או בטור.
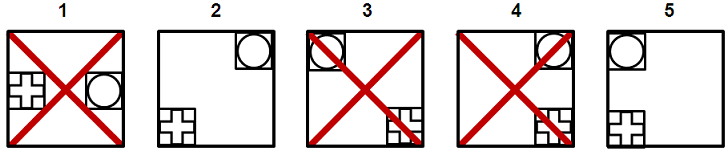
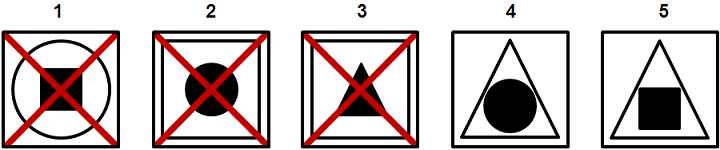
שאלה לדוגמא - איחוד/חיתוך:
תשובות אפשריות:
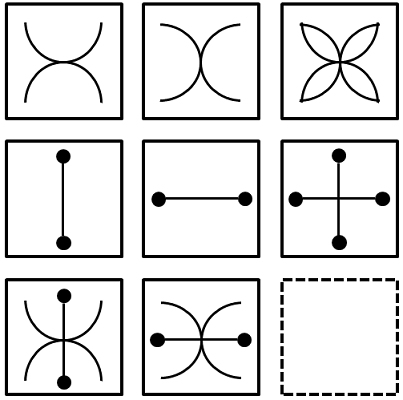
מטריצות: תזוזה/תנועה
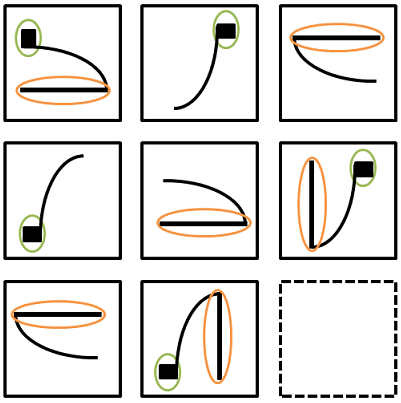
שאלות רבות במבחן המטריצות הן מסוג תזוזה/תנועה. בשאלות אלו יש אלמנט שנע מימין לשמאל ולהפך (בשורה), או מלמטה למעלה ולהפך (בטור). עלינו לזהות את האלמנט שנע ואת כיוונו. אם יש מספר אלמנטים שזזים, נתבונן בתזוזה של כל אחד מהם בנפרד ולאחר מכן ננסה להרכיב את הצורה בשלמותה.
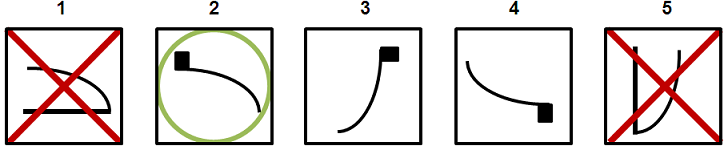
שאלה לדוגמה - תזוזה/תנועה
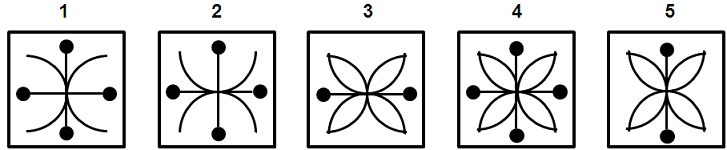
תשובות אפשריות:
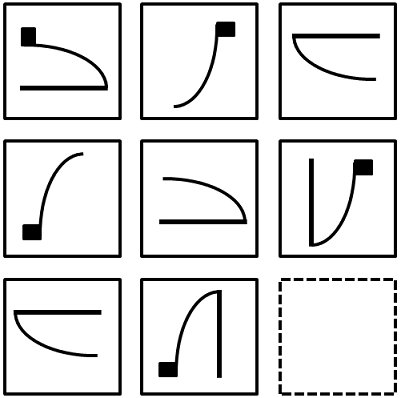
מטריצות: טכניקת הפרדת אלמנטים
אחת הטכניקות שעוזרות בפתרון שאלות מטריצות היא טכניקת הפרדת אלמנטים. בטכניקה זו אנו מתבוננים בנפרד בכל אלמנט שקיים בצורה, ומנסים לבחון "מה קורה" לו. גם בשאלות הקודמות השתמשנו בטכניקה זו, ובעצם כמעט בכל שאלה צורנית משתמשים בטכניקה הזאת.
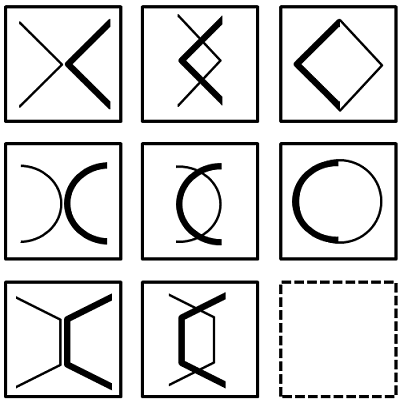
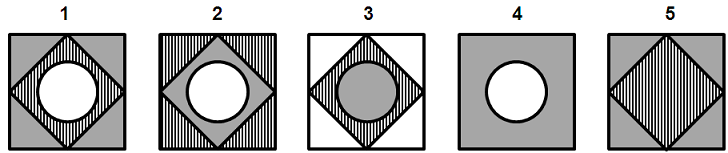
שאלה לדוגמה - טכניקת הפרדת אלמנטים
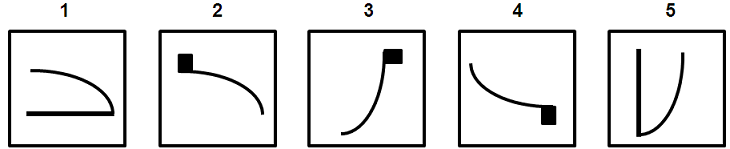
תשובות אפשריות:
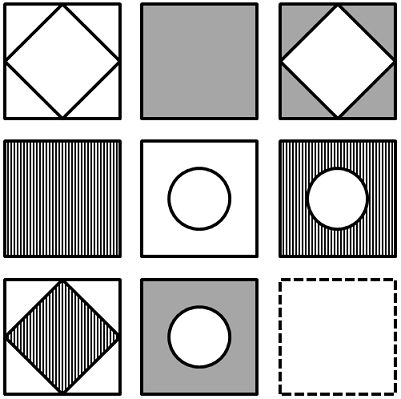
מטריצות: טכניקת בדיקת חוקיות
כאמור, בשאלות צורניות בכלל, ובמטריצות בפרט, יש חוקיות מסוימת אשר מתקיימת בין הצורות. החוקיות יכולה להתבטא בתזוזת אלמנטים, בחיבור אלמנטים ועוד. לעיתים החוקיות הזאת מורכבת מעט יותר. בדוגמא שלפנינו ננסה למצוא את החוקיות של המטריצה ולנסח אותה. לאחר מכן נבדוק אותה, ובשלב האחרון ניישם אותה כדי למצוא את הצורה החסרה.
שאלה לדוגמה - טכניקת בדיקת חוקיות
תשובות אפשריות:
כל מה שאתם צריכים כדי להצליח במבחני הקבלה שלכם
צורות בשורה
בשאלות מסוג זה יוצגו בפניכם רצף של צורות או איברים, המופיעים בשורה. עליכם לזהות את החוקיות העומדת מאחורי הרצף ולזהות מהו האיבר הבא בברצף. כדי לענות על שאלות אלו, יש להסתכל על שני האיברים הראשונים בסדרה, ולזהות מה הקשר ביניהם. לאחר מכן כדאי לנסות ליישם את הקשר הזה בשאר האיברים. גם כאן מומלץ להשתמש בטכניקת הפרדת אלמנטים, שכן לעיתים במעבר מצורה לצורה, חלק מהאלמנטים משתנים.
נתמקד בשני סוגים של שאלות צורות בשורה: "תזוזת אלמנטים" ו"צורות מנבאות".
צורות בשורה: תזוזת אלמנטים
בשאלות אלו ישנם מספר אלמנטים בכל צורה, ותזוזת כל אלמנט מתאפיינת בחוקיות שונה. על כן, עלינו להשתמש בטכניקת הפרדת אלמנטים כדי לזהות את החוקיות אשר מתקיימת בכל אלמנט.
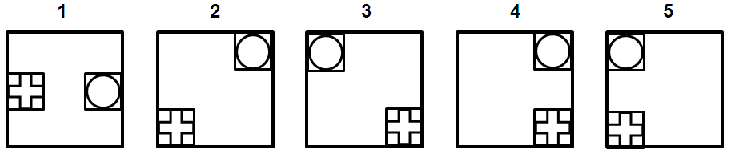
שאלה לדוגמה - תזוזת אלמנטים

תשובות אפשריות:
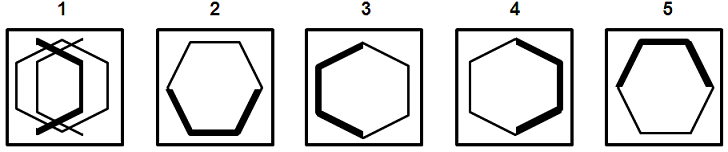
צורות בשורה: צורות מנבאות
בשאלות מסוג זה נראה מספר צורות, המופיעות זו בתוך זו. לרוב צורה מסוימת, המשמשת כאלמנט באחד מהאיברים, מנבאת הופעה של אותה צורה באיבר שונה.
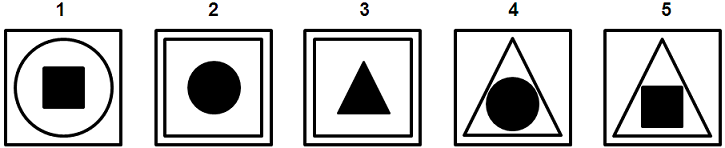
שאלה לדוגמה - צורות מנבאות

תשובות אפשריות:
אל תיתנו למבחן להפתיע אתכם