המבחן הפסיכוטכני פוגש אותנו בקבלה למסגרות שונות לאורך החיים - בצו הראשון, בקבלה למכללות ובמבחני מיון בקבלה לשוק העבודה (אדם מילא, קינן שפי, פילת, לוגיפס ועוד). מדובר על אחד הכלים הנפוצים ביותר למיון וסינון, שמורכב משורה של מבחנים מילוליים, צורניים וכמותיים.
בעמוד הבא תוכלו למצוא מידע חשוב על המבחן ואיך נראים הפרקים הנפוצים בו, וגם לקבל טעימה עם כמה שאלות לדוגמא.
מהו מבחן פסיכוטכני?
מבחן פסיכוטכני הוא כלי סינון ומיון שנועד למדוד את היכולות הקוגניטיביות וצורות החשיבה של מועמדים למקומות עבודה, מוסדות לימודים, ולתפקידים בצה"ל. זהו מבחן אינטנסיבי, שהרכבו משתנה בהתאם ליכולות שהוא נועד לבדוק, כאשר לרוב הוא יורכב משאלות ותרגילים הקשורים בחשיבה צורנית, מילולית וכמותית.
מבחן פסיכוטכני נועד להעריך כישורים ויכולות קוגניטיביות באמצעות פתרון בעיות חשבוניות, שאלות זיכרון, תפיסה מרחבית, זריזות ודיוק. מטרת ההערכה הזו היא לנבא פוטנציאל התאמה לתפקיד, משרה או תחום לימודי.
היום רוב המבחנים הפסיכוטכניים הם ממוחשבים, כאשר אחד האתגרים המשמעותיים של המבחן הפסיכוטכני הוא הגבלת הזמן. בדרך כלל לכל שאלה נתון זמן מענה קצרצר - לפעמים פחות מדקה - מה שדורש מיומנות גבוהה וחשיבה חדה ומהירה. המבחן יכול לנוע בין 30 דקות למספר שעות, כתלות במספר הנושאים הנבדקים ובמורכבות המבחן.
פרקי המבחן הפסיכוטכני - שאלות לדוגמא והסברים
מבחנים כמותיים
מבחנים כמותיים בודקים את יכולת ההסקה הכמותית, את אופן ניתוח המידע, את היכולת להסיק מסקנות מגרפים ומטבלאות מורכבות, ואת מידת השליטה וההבנה בתחום המתמטיקה. לרוב יוצגו במבחנים אלה שאלות אמריקאיות והם יכללו מבחני ידע בחשבון בסיסי, מבחני הסקה, סדרות, בעיות דרך והספק ועוד. בדרך כלל, מדובר על מבחנים רבי-ברירה ("אמריקאים"). בחלק מהמבחנים הפסיכוטכניים מותר להשתמש במחשבון, בדפי טיוטה ובכלי כתיבה - מומלץ לבדוק מראש אם זה המקרה במבחן שלכם.
הנה כמה דוגמאות לשאלות בתחום הכמותי:
שאלה 1 לדוגמא (דרך והספק)
אוטובוס יוצא מנקודה A לנקודה B במהירות 100 קמ"ש. בכמה זמן יעבור את הדרך אם המרחק בין A ל-B הוא 120 ק"מ?
- 1.2 שעות
- שעה אחת
- 0.8 שעות
- 12 דקות
פתרון והסבר:
התשובה הנכונה היא (1).
אם האוטובוס נוסע במהירות של 100 קמ"ש, מכאן שבכל שעה הוא עובר דרך של 100 ק"מ (דרך = זמן x מהירות). במקרה זה על האוטובוס לעבור דרך של 120 ק"מ, ולכן בהכרח זמן נסיעתו יהיה גדול משעה. בהתבוננות על אפשרויות התשובה בשאלה זו ניתן לראות כי רק תשובה (1) מתאימה לדרישה זו.
אפשר גם לחשב במדויק. ידוע כי המהירות = 100 קמ"ש והדרך = 120 ק"מ.
לפי הנוסחה של זמן X מהירות = דרך:
זמן = דרך חלקי מהירות = 1.2 = 100 / 120
לכן התשובה הנכונה היא 1.2 שעות.
שאלה 2 לדוגמא (גרפים)
לפניכם גרף המתאר את אחוזי הגידול של הנסועה השנתית (קילומטרז'), מצבת כלי הרכב, שטח הכבישים ואורכם בשנים 1990 עד 2006. הבסיס להתייחסות הוא שנת 1990, המיוצגת ב-100%.
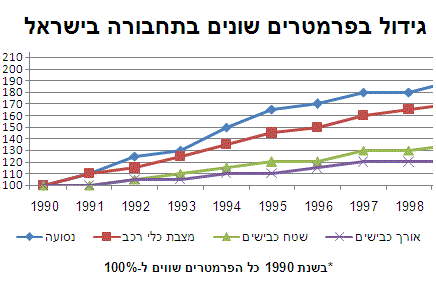
מהו אחוז הגידול בשטח הכבישים שחל משנת 1990 ועד לשנת 1998?
- 10%
- 20%
- 30%
- 40%
פתרון והסבר:
התשובה הנכונה היא (3).
מכיוון שנתון שהגרף המקורי הוא באחוזים ולא במספרים מוחלטים, אין צורך להשתמש בנוסחת האחוז כדי לחשב את השינוי - די בחישוב פשוט. על פי המדדים בשנת 1990 היה שטח הכבישים 100, ואילו בשנת 1998 - 130.
לכן התשובה הנכונה היא 30%.
שאלה 3 לדוגמא (הסקה מתרשים)
לפניכם תרשים המתאר את מספר הקופים בגני החיות בישראל לאורך המאה ה-20:
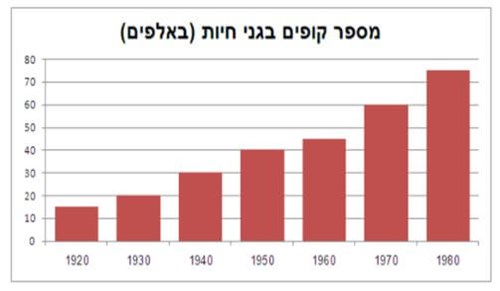
באיזו שנה נרשם הגידול היחסי הגבוה ביותר במספר הקופים ביחס לעשור שקדם לה?
- 1940
- 1950
- 1970
- 1980
- אי אפשר לדעת
פתרון והסבר:
התשובה הנכונה היא (1).
נבין תחילה מה אנו נשאלים. אנו נדרשים למצוא את הגידול היחסי באוכלוסיית הקופים בין עשורים שונים (עשור הוא פרק זמן של 10 שנים). גידול יחסי הוא גידול ביחס לגורם אחר (במקרה זה הגידול יהיה ביחס למספר הקופים בעשור הקודם).
כלומר אם נתבונן בשתי העמודות השמאליות בתרשים המייצגות את מספר הקופים בעשור שבין 1930-1920, נוכל לראות כי שיעור הגידול הוא 5,000 קופים בעוד הגידול היחסי בעשור זה הוא:
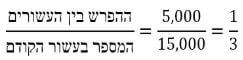
* 15,000 הוא מספר הקופים בתחילת העשור, כלומר ב-1920.
לאחר שהבנו מה נשאלנו, נעבור על התשובות ונבדוק מה הגידול היחסי בכל אחד מהעשורים הרלוונטיים.
נזכיר שכל הנתונים הם באלפים, אך כדי להקל עלינו את מלאכת החישוב נעבוד עם מספרים פשוטים, ללא תוספת האלפים (10 במקום 10,000 וכדומה).
תשובה (1): בשנים 1930 עד 1940 אפשר לראות כי הגידול הוא 10.
מכאן שהגידול היחסי הוא:
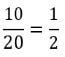
תשובה (2): בשנים 1940 עד 1950 אפשר לראות כי הגידול הוא 10.
מכאן שהגידול היחסי הוא:
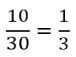
תשובה (3): בשנים 1960 עד 1970 אפשר לראות כי הגידול הוא 15.
מכאן שהגידול היחסי הוא:
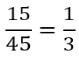
תשובה (4): בשנים 1970 עד 1980 אפשר לראות כי הגידול הוא 15.
מכאן שהגידול היחסי הוא:
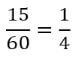
אפשר לראות כי:
הערה: אפשר לפתור שאלה זו גם בצורה אינטואיטיבית, ומומלץ לעשות זאת במקרה של מחסור בזמן.
מכיוון שהגידולים בין העשורים שווים פחות או יותר, ככל שהמספר ההתחלתי קטן יותר, כך הגידול היחסי גבוה יותר. לפיכך סביר שדווקא בעשורים המוקדמים הגידול היחסי היה גבוה יותר לעומת העשורים המאוחרים, שבהם מספר הקופים היה גבוה בהרבה ממספרם בעשורים המוקדמים.
שאלה 4 לדוגמא (סדרות)
מצאו את המספר/ים החסרים בסדרה:
? | ? | 12 | 68 | 8 | 34 | 4 | 17
1. 102 , 42
2. 16 , 108
3. 102 , 136
4. 16 , 136
פתרון והסבר:
התשובה הנכונה היא (4).
הסדרה שלפנינו מורכבת משתי סדרות שונות שאיבריהן מופיעים לסירוגין באופן הבא:
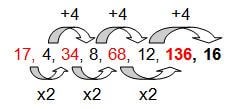
(i) האיברים במקומות האי-זוגיים (מסומנים באדום) יוצרים סדרה ובה הפער בין זוג איברים הוא כפל ב-2.
(ii) האיברים במקומות הזוגיים יוצרים סדרה ובה הפער בין זוג איברים הוא חיבור של 4.
מבחנים מילוליים
מבחנים מילוליים בוחנים יכולות כמו הבנת הנקרא, הסקת מסקנות, פרשנות ומידת השליטה של המועמדים בשפה העברית. את כל אלה יבחנו שאלות הבנה מתוך טקסט, אנלוגיות מילוליות, שאלות לוגיקה, מבחני הבנת הוראות, דקדוק ואיות ועוד. שימו לב כי חלק מהמבחנים כוללים גם פרקי אנגלית, המורכבים משאלות בהבנת הנקרא, ניסוח מחדש והשלמת משפטים באנגלית.
קבלו כמה דוגמאות לשאלות בתחום המילולי:
שאלה 1 לדוגמא (הבנת הנקרא)
להלן קטע קריאה קצר, ולאחריו היגד הנוגע לקטע. עליכם לקבוע אם ההיגד נכון, לא נכון או שלא ניתן לדעת אם הוא נכון מכיוון שחסרים נתונים.
קטע קריאה:
מטוסים שטסים לחו"ל משתמשים במפות נתיבים בינלאומיים. שינוי במספר המטוסים ובנתיבי התעופה מחייב הכנת מפות ידניות חדשות מדי חודש. מכשיר חדש לשרטוט מפות שפותח לאחרונה על ידי חברת אלביט מאפשר אחסנת כל האינפורמציה האווירית והצגת כל הנתיבים האפשריים על פי כמות המטוסים והטיסות בזמן נתון. המכשיר החדש שפותח נותן פתרון גם לטייסי חיל האוויר שטסים בנתיבים צבאיים פנים-ארציים ומונע תאונות והתנגשויות בין מטוסים.
היגד: השיטה החדשה שפותחה משפרת את בטיחות הטיסות.
תשובות אפשריות:
- נכון
- לא נכון
- לא ניתן לדעת
שאלה 1 לדוגמא (הבנת הנקרא)
להלן קטע קריאה קצר, ולאחריו היגד הנוגע לקטע. עליכם לקבוע אם ההיגד נכון, לא נכון או שלא ניתן לדעת אם הוא נכון מכיוון שחסרים נתונים.
קטע קריאה:
מטוסים שטסים לחו"ל משתמשים במפות נתיבים בינלאומיים. שינוי במספר המטוסים ובנתיבי התעופה מחייב הכנת מפות ידניות חדשות מדי חודש. מכשיר חדש לשרטוט מפות שפותח לאחרונה על ידי חברת אלביט מאפשר אחסנת כל האינפורמציה האווירית והצגת כל הנתיבים האפשריים על פי כמות המטוסים והטיסות בזמן נתון. המכשיר החדש שפותח נותן פתרון גם לטייסי חיל האוויר שטסים בנתיבים צבאיים פנים-ארציים ומונע תאונות והתנגשויות בין מטוסים.
היגד: השיטה החדשה שפותחה משפרת את בטיחות הטיסות.
תשובות אפשריות:
- נכון
- לא נכון
- לא ניתן לדעת
פתרון והסבר:
התשובה הנכונה היא (1).
בקטע מצוין שהמכשיר החדש מונע תאונות והתנגשויות בין מטוסים, ולכן ההיגד נכון.
שאלה 2 לדוגמא (לוגיקה)
אם אין פנס שאינו צהוב ואין נר שאינו פנס, אזי תמיד נכון ש-
- אין צהוב שאינו פנס
- כל נר הוא צהוב
- כל צהוב הוא גם נר
- אף אחת מהנ"ל
פתרון והסבר:
התשובה הנכונה היא (2).
מהמשפט: "אם אין פנס שאינו צהוב", ניתן להסיק כי כל הפנסים הם צהובים, ולכן קבוצת הפנסים מוכלת בתוך קבוצת הצהובים. מהמשפט: "אין נר שאינו פנס", נסיק כי כל הנרות הם פנסים, ולכן קבוצת הנרות מוכלת בתוך קבוצת הפנסים (ולכן היא מוכלת גם בתוך קבוצת הצהובים).
נצייר זאת כך:
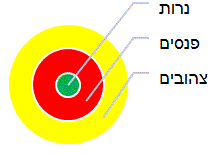
עלינו לקבוע איזה מהמשפטים הבאים תמיד נכון. לשם כך נבחן את האפשרויות המוצעות לנו:
- תשובה (1): "אין צהוב שאינו פנס" – לא בהכרח נכונה. מהציור ניתן לראות כי קבוצת הפנסים מוכלת בתוך קבוצת הצהובים, ולא להפך. ייתכן שהחפיפה בין שתי הקבוצות מלאה, אך אין בידינו מספיק נתונים כדי לקבוע זאת. לפיכך, לא ניתן לקבוע שמשפט זה נובע מן הנתונים.
- תשובה (2): "כל נר הוא צהוב" – נכונה. מהציור ניתן לראות כי קבוצת הנרות מוכלת בתוך קבוצת הפנסים, וזו מוכלת בתוך קבוצת הצהובים. כלומר, גם קבוצת הנרות מוכלת בתוך קבוצת הצהובים, ולכן כל נר הוא צהוב.
- תשובה (3): "כל צהוב הוא גם נר" – לא בהכרח נכונה. מהציור ניתן לראות כי קבוצת הנרות מוכלת בתוך קבוצת הצהובים, ולא להפך. ייתכן שהחפיפה בין שתי הקבוצות מלאה, אך אין בידינו מספיק נתונים כדי לקבוע זאת. לפיכך, לא ניתן לקבוע שמשפט זה נובע מן הנתונים.
- תשובה (4): "אף אחת מהנ"ל" – אינה רלוונטית, מאחר שתשובה (2) נכונה.
מבחני צורות
מבחני צורות בוחנים יכולת איתור ויישום חוקיות צורנית. במבחנים צורניים יוצגו לכם סדרת צורות במבנה מסוים, ואתם תידרשו להסיק מהי הצורה המשלימה את הסדרה. כדי לעשות זאת, עליכם להבין במהירות את הקשר בין הצורות המוצגות, באמצעות הסקה לוגית. למעשה, מבחני צורות לא נסמכים על ידע מוקדם, אלא על יכולת תפיסה ולוגיקה, והם כוללים מבחני מטריצות, צורות בשורה, שטיחים, צורות בסבך, מבחני קוביות ועוד. חלק מהמבחנים בודקים תפיסה מרחבית, ומיועדים בעיקר לתפקידים בעלי אופי טכני.
קבלו כמה שאלות לדוגמא מהתחום הצורני:
שאלה 1 לדוגמא (צורות בשורה)
בחרו את הצורה שמשלימה באופן הגיוני את הסדרה.
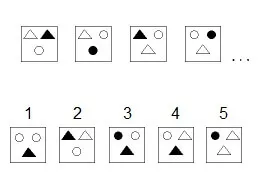
פתרון והסבר:
התשובה הנכונה היא (4).
סדרה זו מורכבת מריבועים שבתוכם מתקיימות תנועתיות של משולשים ועיגולים בצבעים שחור ולבן ורוטציה ביניהם.
בריבוע תמיד יש שתי צורות מאותו הסוג, אחת בצבע לבן, ואחת בצבע שחור. הצורה הבודדת מהסוג השני תמיד מופיעה בצבע לבן. בצעד הבא הצורה השחורה תעלם ובמקומה תמוקם הצורה הסמוכה אליה מהסוג השני, בצבע לבן (כך שאם העיגול השחור נעלם, במקומו יהיה משולש לבן), ובמקומה יהיה שכפול של הצורה שזזה, בצבע שחור.
בצורה הראשונה יש שני משולשים - אחד שחור ואחד לבן - נוסף על עיגול לבן. בצעד הבא המשולש השחור ייעלם ובמקומו יבוא העיגול הלבן. במקום שבו היה העיגול הלבן יופיע עיגול שחור. כעת בצורה השנייה יש שני עיגולים, אחד שחור ואחד לבן, נוסף על משולש לבן. בצעד הבא על העיגול השחור להיעלם ובמקומו יבוא המשולש הלבן. במקום שבו היה המשולש הלבן יופיע משולש שחור. בצורה הרביעית ניתן לראות כי יש שני עיגולים - אחד שחור ואחד לבן - נוסף על משולש לבן. בצעד הבא על העיגול השחור להיעלם, ובמקומו יבוא המשולש הלבן. במקום שבו היה המשולש הלבן יופיע כעת משולש שחור.
שאלה 2 לדוגמא
בחר/י את הצורה המשלימה את המטריצה הבאה:
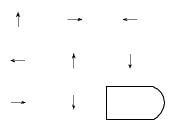
פתרון והסבר:
התשובה הנכונה היא (1).
בכל שורה, במעבר מצורה לצורה, החץ נע פעם אחת ב-90 מעלות בכיוון השעון, ובפעם נוספת ב-180 מעלות.
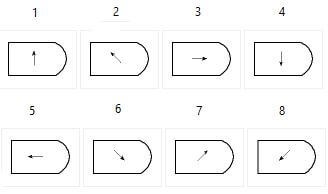
שאלה 3 לדוגמא
בחר/י מבין הצורות למטה את הצורה המתאימה להשלמת הרצף משמאל לימין:

פתרון והסבר:
התשובה הנכונה היא (3).
במעבר מהאיבר הראשון לאיבר השני אפשר לראות כי המחוג הימני זז ב-45 מעלות בכיוון השעון, ואילו המחוג השמאלי זז ב-45 מעלות נגד כיוון השעון:

מכך אפשר להסיק כי במעבר מאיבר לאיבר מחוגים נעים 45 מעלות בכיוון השעון ונגד כיוון השעון בהתאמה.
הערה: מכיוון ששני המחוגים זהים בצורתם ובאורכם, בצורה הרביעית - כאשר שניהם מצביעים כלפי מטה - הם נראים כחץ בודד, אך למעשה הם מונחים זה על גבי זה.

